When Can You Use the Normal Approximation to the Binomial Distribution
The normal approximation to the binomial is when you use a continuous distribution (the normal distribution) to gauge a discrete distribution (the binomial distribution). According to the Central Limit Theorem, the sampling distribution of the sample means becomes approximately normal if the sample size is large plenty.
Normal Approximation to the Binomial: n * p and n * q Explained
Need assistance with a homework question? Bank check out our tutoring page!
The outset step into using the normal approximation to the binomial is making sure you lot have a "large plenty sample". How large is "large enough"? You effigy this out with two calculations: n * p and n * q .
- due north is your sample size,
- p is your given probability.
- q is merely ane – p. For example, let'southward say your probability p is .6. Y'all would find q by subtracting this probability from i: q = 1 – .6 = .4. Percentages (instead of decimals) can make this a lilliputian more understandable; if you have a 60% take chances of it raining (p) then there's a twoscore% probability it won't rain (q).
When north * p and n * q are greater than five, you can use the normal approximation to the binomial to solve a problem.
Normal Approximation: Example #1 (Video)
Picket the video for an case:
Tin't see the video? Click here.
Normal Approximation: Example #2
60 two percent of 12th graders nourish school in a particular urban school commune. If a sample of 500 12th course children are selected, find the probability that at to the lowest degree 290 are actually enrolled in school.
Part ane: Making the Calculations
Stride one: Notice p,q, and northward:
- The probability p is given in the question every bit 62%, or 0.62
- To discover q, decrease p from 1: 1 – 0.62 = 0.38
- The sample size n is given in the question as 500
Footstep 2: Figure out if you can utilize the normal approximation to the binomial. If n * p and north * q are greater than 5, so you lot can use the approximation:
n * p = 310 and due north * q = 190.
These are both larger than 5, so you can use the normal approximation to the binomial for this question.
Pace iii: Find the mean, μ past multiplying due north and p:
n * p = 310
(Yous really figured that out in Step ii!).
Step 4: Multiply step 3 by q :
310 * 0.38 = 117.8.
Footstep five: Take the square root of step 4 to get the standard deviation, σ:
√(117.8)=10.85
Annotation: The formula for the standard deviation for a binomial is √(n*p*q).
Part 2: Using the Continuity Correction Factor
Step 6: Write the trouble using correct notation. The question stated that we need to "detect the probability that at least 290 are actually enrolled in school". And then:
P(Ten ≥ 290)

Listing of continuity correction factors.
Step seven: Rewrite the problem using the continuity correction cistron:
P (10 ≥ 290-0.5) = P (X ≥ 289.5)
Note: The CCF table is listed in the higher up image, but if you haven't used it before, yous may want to view the video in the continuity correction gene article.
Step 8: Draw a diagram with the mean in the center. Shade the area that corresponds to the probability you are looking for. We're looking for X ≥ 289.five, so:
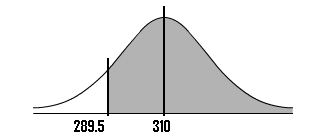
Step ix: Find the z-score.
Y'all can notice this by subtracting the mean (μ) from the probability yous establish in pace 7, then dividing by the standard difference (σ):
(289.5 – 310) / 10.85 = -i.89
Step x: Look up the z-value in the z-table:
The surface area for -1.89 is 0.4706.
Step 11: Add .5 to your answer in step ten to notice the total surface area pictured:
0.4706 + 0.v = 0.9706.
That's it! The probability is .9706, or 97.06%.
Cheque out our YouTube channel for hundreds more statistics help videos!
References
Kotz, Southward.; et al., eds. (2006), Encyclopedia of Statistical Sciences, Wiley.
Everitt, B. S.; Skrondal, A. (2010), The Cambridge Lexicon of Statistics, Cambridge University Press.
Vogt, W.P. (2005). Dictionary of Statistics & Methodology: A Nontechnical Guide for the Social Sciences. SAGE.
Lindstrom, D. (2010). Schaum's Easy Outline of Statistics, 2nd Edition (Schaum's Easy Outlines) 2nd Edition. McGraw-Hill Education
---------------------------------------------------------------------------
Need aid with a homework or test question? With Chegg Study, you can get footstep-by-stride solutions to your questions from an expert in the field. Your first 30 minutes with a Chegg tutor is free!
Comments? Need to post a correction? Delight post a comment on our Facebook folio .
Source: https://www.statisticshowto.com/probability-and-statistics/binomial-theorem/normal-approximation-to-the-binomial/#:~:text=When%20n%20*%20p%20and%20n,binomial%20to%20solve%20a%20problem.
0 Response to "When Can You Use the Normal Approximation to the Binomial Distribution"
Post a Comment